Starvation, Submergence, and NPSH
When a pump is failing, often by wear or abuse on the impeller, shaft, or front thrust washer, it is most often due to poor suction conditions. You can often hear it happening if the pump starts making a louder noise or a cracking/popping noise. The three Suction Side Problems to look for are Starvation, Submergence, and NPSH (Net Positive Suction Head). Starvation is the most common, followed by Submergence, and then NPSH. It is possible that it may be a combination of two of them or even three. To determine if one is suffering from one of these three problems, one should first check for Starvation, then Submergence, and then NPSH. This manual will show how to check for each.
Starvation:
Starvation is when the pump is trying to put out more than is coming in. In its most extreme form, the pump is being run dry. If the pump can do 20GPM at 30 feet, the pump will always try to do 20GPM at 30 feet, even if you only have 18GPM coming in. The larger the difference between what the pump is trying to do and what it has coming in, the more damage the pump will suffer. In order to calculate what is coming in, one must determine two things.
- What is the friction loss and velocity on the suction side for the target flow rate leaving the pump?
- What is the liquid level over the pump?
To determine your friction loss on the suction side, you should use an online friction loss calculator. http://www.freecalc.com/fricfram.htm
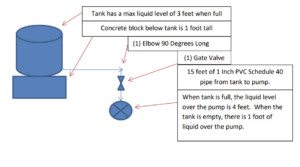
Using the system example given above, from the tank to the pump you have 15 feet of 1 inch PVC pipe schedule 40, with (1) 90 degree LR elbow, and (1) gate valve. Assume you want 20GPM leaving the pump. Insert these numbers into the online friction loss calculator and press “calculate pressure drop”. The screen states your Head Loss (friction loss) is 3.5 feet and your velocity is 7.43 feet per second. You have now calculated your friction loss and velocity for 20GPM.
For the liquid level over the pump, measure the liquid level over the inlet of the pump. It is important to get the level over the liquid both when at its highest and lowest. When the tank is full, the liquid level is 4 feet over the pump. When the tank is empty, there is only 1 foot of liquid level over the pump. When the liquid level is 4 feet, the 4 feet of liquid can overcome the friction loss of 3.5 feet for 20GPM. When it is only 1 foot of liquid, 20GPM will not overcome the friction loss of 3.5 feet, so you will get less than 20GPM. Playing with the calculator, by changing the flow rate, only at 10GPM will the Head Loss (friction loss) decreases to 1 foot and the velocity decreases to 3.71 feet per second.
Submergence:
Submergence is when the pump sucks in air thru a vortex. Vortexes can take many different shapes, please see this link. http://www.pumpfundamentals.com/help11.html
To determine if a vortex is being formed, one must determine two things.
- What is the velocity of the incoming liquid?
- How much liquid level is over the pump?
The velocity of the liquid coming into the pump can be determined by the same friction loss calculator used earlier. http://www.freecalc.com/fricfram.htm
Using the same suction conditions as previously given, for 20GPM the velocity is 7.43 feet per second and at 10GPM is 3.71 feet per second.
For the liquid level over the pump, again using the same suction side conditions as before, when the tank is full, there is 4 feet of liquid over the pump. When empty, there is only 1 foot of liquid over the pump.
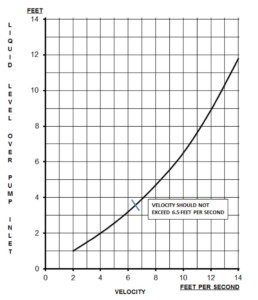
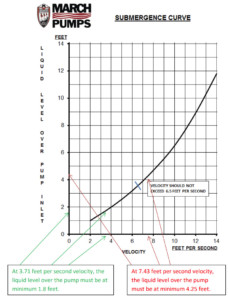
Using the Submergence curve below, find on the horizontal or X Axis the velocity you calculated for 20GPM, which is 7.43 feet per second. Go straight up until you hit the upward sloping line. Then go left and find the number on the vertical or Y Axis. The upward sloping line intersects with 7.43 feet per second velocity approximately around 4.25 feet liquid level over pump suction. This means to prevent a vortex the pump must have 4.25 feet of liquid over it. For this case, because there is only 4 feet of liquid over the pump, a vortex will form. At 10GPM, the velocity is 3.71 feet per second. This upward sloping line intersects with 3.71 feet per second at 1.8 feet, meaning you should have at least 1.8 feet of liquid over the pump inlet to prevent a vortex.
NPSH:
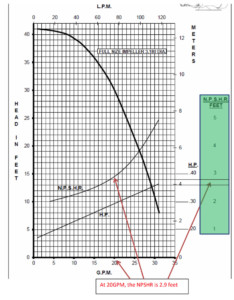
NPSH is short for Net Positive Suction Head. With NPSH, there is always NPSHa and NPSHr. NPSHa is Net Positive Suction Head Available and NPSHr is Net Positive Suction Head Required. NPSHa is something the user must calculate and is unique with each system. NPSHr is always given by the pump manufacturer. The system’s NPSHa must always be greater than the NPSHr to prevent damage to the pump. In the below curve, the NPSHr at 20GPM is approximately 2.9 feet.
To calculate NPSHa the following equation is used:
Atmosphere Pressure (In feet) – Vapor Pressure of Liquid (in feet) + Static Head (in feet) – Suction Friction (In feet)
Let’s calculate the NPSHa for the system example we’ve been using. Assume the system is in Chicago, and the liquid is 100 Fahrenheit water.
- Atmosphere Pressure: To calculate what your atmosphere pressure is, use the following calculator. http://www.mide.com/pages/air-pressure-at-altitude-calculator Use the second equation titled “Calculate Air Pressure at Altitude”. Put in your temperature (use F) and Altitude (use Feet) and press calculate. For this example, let’s use 70 Fahrenheit and the altitude of Chicago at 594 feet (you can determine your altitude by using google). Using 70 Fahrenheit and 594 feet, the air pressure for Chicago is 14.39PSI.
The equation to convert PSI into Feet is: Feet= (PSI X 2.31)/Specific Gravity
So for this example: (14.39 x 2.31)/1.0= 33.2409 Feet *For this specific conversion, do not worry about specific gravity.
33.24 feet- Vapor Pressure of liquid (in feet) + Static Head (in feet) -Suction Friction (In feet)=NPSHa
- Vapor Pressure of Liquid: Let’s assume its 100 Fahrenheit water. Google “Vapor Pressure of Water”. On the first page, this link appears, http://intro.chem.okstate.edu/1515sp01/database/vpwater.html At 100 Fahrenheit water, which is 37.7 Celsius (using a google conversion), the vapor pressure according to this link at 38C is 49.7 mmHG (which is short for Millimeter of Mercury). Use this link, http://www.endmemo.com/sconvert/psimmhg.php to convert 49.7 mmHG to PSI, and doing so it is 0.96 PSI. Convert PSI to head.
Feet= (PSI x 2.31)/Specific Gravity
(0.96 x 2.31)/ 1.0= 2.22 feet
* The specific gravity of water is 1.0 at 68F. At higher temperatures the specific gravity of water does begin to decrease. For example, at 200F, the specific gravity decreases to 0.96. For simplicity, let’s assume for this example at 100F the specific gravity remains 1.0. For a chart of the specific gravity of water at different temperatures, please see this link, http://www.engineeringtoolbox.com/water-temperature-specific-gravity-d_1179.html
33.24 feet- 2.22 feet + Static Head (in feet) – Suction Friction (In feet)=NPSHa
- Static Feet: Static Feet is how much liquid is over the pump. Using the same example we’ve been using, when the tank is full we have 4 feet of liquid over the pump.
33.24 feet- 2.22 feet + 4 feet – Suction Friction (In feet) =NPSHa
- Suction Friction: Suction Friction is the friction loss on the suction side of the pump. Using the same example we’ve been using, at 20GPM, the friction loss is 3.5 feet.
33.24 feet- 2.22 feet + 4 feet-3.5 feet= NPSHa
NPSHa= 31.52 feet.
If the NPSHa is 31.52 feet, then as long as the NPSHr is below 31.52 feet, the pump will not suffer damage from a lack of NPSH. March recommends having a minimum 120% or 1.2 safety factor for the NPSHa over the NPSHr. So, in the NPSHr curve on page 4, at 20GPM the NPSHr is 2.9 feet. 2.9 feet times 1.2 is 3.48 feet. As we have 31.52 feet NPSha, we have more than is needed.
NPSH Example 2:
However, what if the temperature of the water is 200F but everything else remains the same?
33.2409 feet- Vapor Pressure of 200 Fahrenheit Water In Feet + 4 feet-3.5 feet= NPSHa
Using the links previously given, 200 Fahrenheit (or 93 Celsius) water has a vapor pressure of 588.6 mmHG. Use this link, http://www.endmemo.com/sconvert/psimmhg.php to convert 588.6 mmHG into PSI, and doing so, it is 11.38 PSI.
For the specific gravity, use the link previously given, http://www.engineeringtoolbox.com/watertemperature-specific-gravity-d_1179.html , and it shows at 200F the specific gravity is 0.96.
Feet= (PSI x 2.31)/Specific Gravity
Feet= (11.38 x 2.31)/0.96
Feet= 27.38
Plug the 27.38 feet into the NPSHa equation.
33.2409 feet- 27.38 feet+ 4 feet-3.5 feet= NPSHa
NPSHa=6.36 Feet.
The 6.36 NPSHa is still over 120% greater than the NPSHr, so the pump will not suffer damage.
Suggestions If Pump is Suffering from Starvation, Submergence, or NPSH:
- The easiest thing to help with Starvation, Submergence, and NPSH is to increase the static head or liquid level over the pump. Try to elevate the tank or lower the pump.
- For all three, use a valve on the discharge, use variable speed to decrease the speed, or trim the impeller diameter, to decrease the GPM leaving the pump.
- Decrease your friction losses for help with Starvation or NPSH. You can decrease your friction losses by minimizing elbows, valves, and keeping the pump as close as you can to the tank.
- For Submergence, consider making or buying an anti-vortex cap for the tank to help break up the vortex.
Reminders:
- For most applications, the pump will encounter one or a combination of the three Suction Side problems at some point. The key is to minimize the severity and the time the pump will encounter the Suction Side Problems.
- Determining if the pump is experiencing any of these Suction Side Problems is difficult, even using this manual as a template. Feel free to contact a March Pump Distributor or a March Pump engineer if you will like further assistance.
Submergence Curve